Block Cholesky Decomposition

A substantial improvement on the prior Cholesky decomposition can be made by using blocks rather than recursing on the scalar. This allows us to work in much large chunks and even makes the recursive formulation competitive.

Here is the recursive code:

function U = chol_sec_block(A)
% Author: Stephen Conover
% Date: January 2014
% This function uses a block formulation to recursively computer the
% cholesky decomposition of a NxN hermitian matrix A.

blockSize  = min(96, length(A));

if(isempty(A))
U = [];
return;
end;

U = zeros(size(A));

% Computer the blocks:
Utl = chol_sec_nr(A(1:blockSize, 1:blockSize));
Utr = (Utl^-1)'*A(1:blockSize, blockSize+1:end);

U(1:blockSize,1:blockSize) = Utl;
U(1:blockSize,blockSize+1:end) = Utr;

% Do the recursion.
Sbr = A(blockSize+1:end, blockSize+1:end) - Utr'*Utr;
U(blockSize+1:end, blockSize+1:end) = chol_sec_block(Sbr);

end

and here is the non-recursive:

function U = chol_sec_nr_block(A)
% Author: Stephen Conover
% Date: January 2014
% This function uses a block formulation to non-recursively computer the
% cholesky decomposition of a NxN hermitian matrix A.

% check for Empty:
if(isempty(A))
U = [];
return;
end;

% Intialize output:
N = length(A);
U = zeros(size(A));

blockSize = 96;
myOffset = -blockSize;
inds = 1:blockSize;

% Loop through each chunk of blocksize:
for n = 1:N/blockSize

myOffset = (n-1)*blockSize;

Utl = chol_sec_nr(A(myOffset + inds, myOffset + inds));
Utr = (Utl^-1)'*A(myOffset + inds, (n*blockSize+1):N);

U(inds + myOffset,inds+myOffset) = Utl;
U(myOffset + inds, (n*blockSize+1):N) = Utr;

Sbr = A(myOffset+1+blockSize:N, myOffset+1+blockSize:N) - Utr'*Utr;
A(myOffset+1+blockSize:N, myOffset+1+blockSize:N)  = Sbr;

end

% finish off the rest of the computation < blockSize int he bottom right:
if(mod(N, blockSize) > 0)
U(myOffset+1+blockSize:end, myOffset+1+blockSize:end) = chol_sec_nr(A(myOffset+1+blockSize:end, myOffset+1+blockSize:end));
end

end

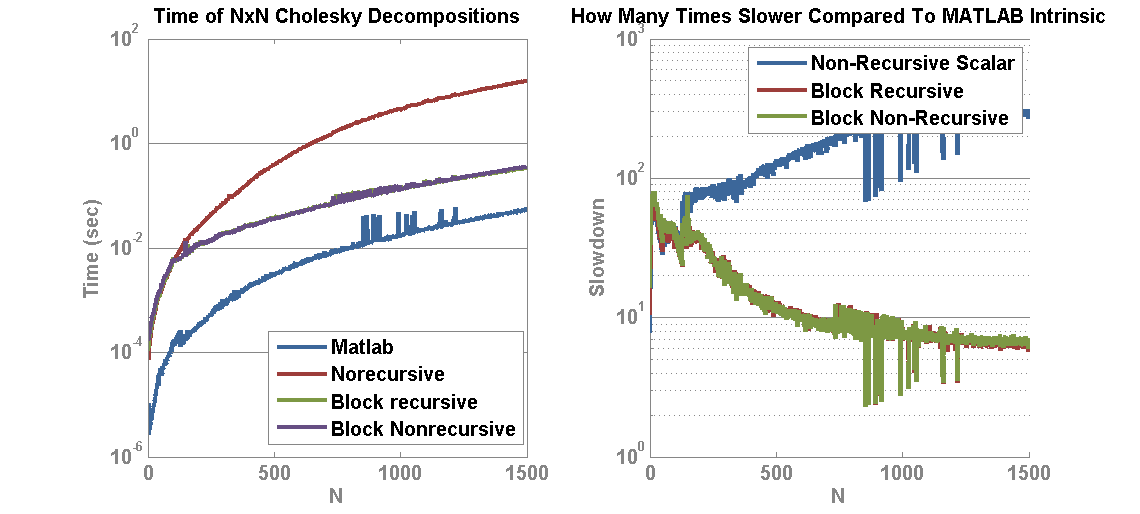
The following plot compares the original scalar formulation, the new block recursive/non-recursive formulation, and the MATLAB intrinsic. The MATLAB intrinsic still spanks the scripting code but I believe we may see this come close to parity when it is implemented in C++.

Example speeds at 1500 x 1500 are:

1. Original Custom Recursive Scalar Decomposition time: 15.79s
2. Custom Recursive Cholesky Block Decomposition time: 0.3571s
3. Custom Non-Recursive Cholesky Block Decomposition time: 0.3384s
4. MATLAB Intrinsic Cholesky Decomposition time: 0.0510s