linear algebra – Stephen Conover

May 12, 2015May 12, 2015

Matlab R2014b CPU and GPU Matrix Multiply Time Comparison

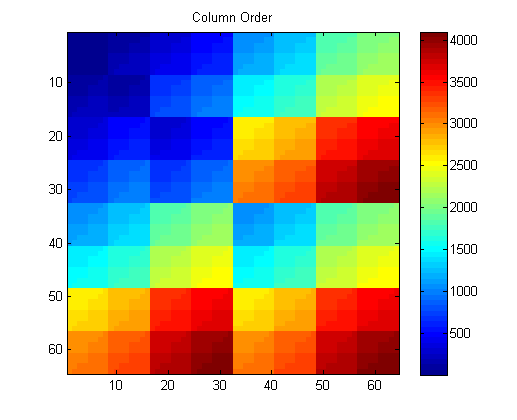
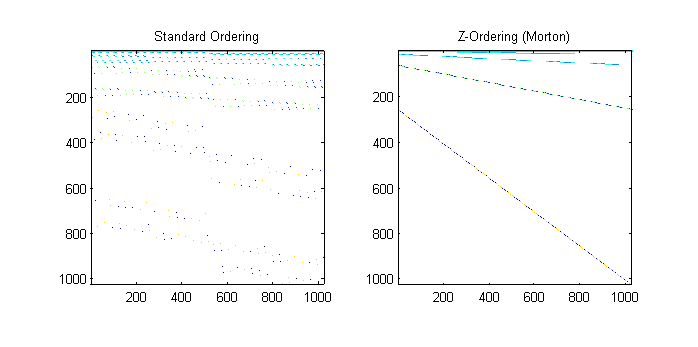
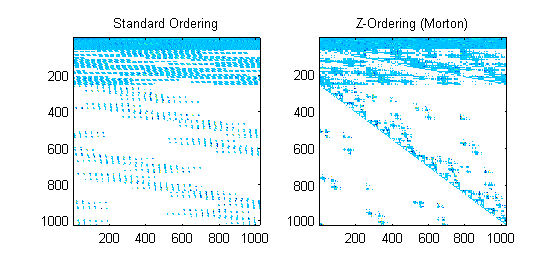
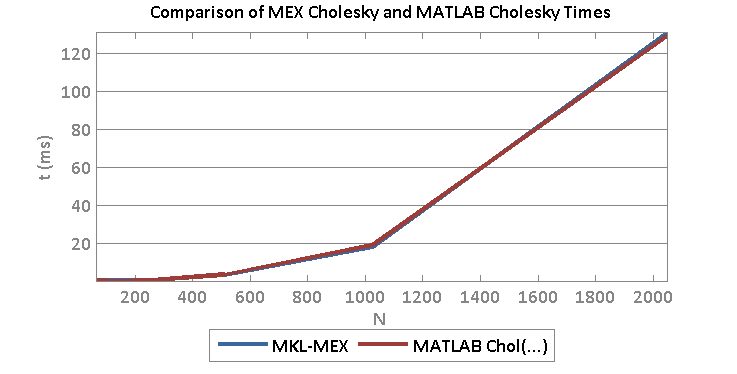
Matlab has incorporated GPU processing on the parallel computing toolbox and you can create GPU array objects using the gpuArray(…) function in MATLAB. I created a brief script to compare matrix multiply of a 2048 x 2048 matrix against a vector. Ordinarily, the CPU operations see reasonable speedup (~2x) from moving from double to single precision values. However, moving to the GPU implementation results in a speedup of 6.8x for Double and 5.6x for Single! This means that if you can take a matrix-vector multiply that is double precision and convert it to single precision GPU version, you may see a gain of nearly 14x.

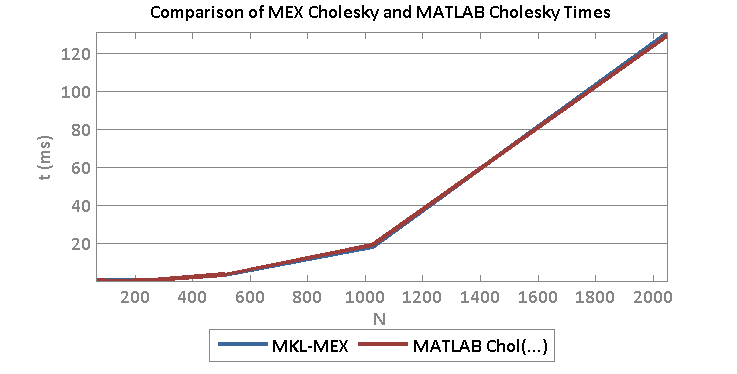
The following we generated in Matlab R2014b on an i7-4770 3.5 Ghz CPU (8 CPUs) with 16GB Ram and a Geforce GTX 750.

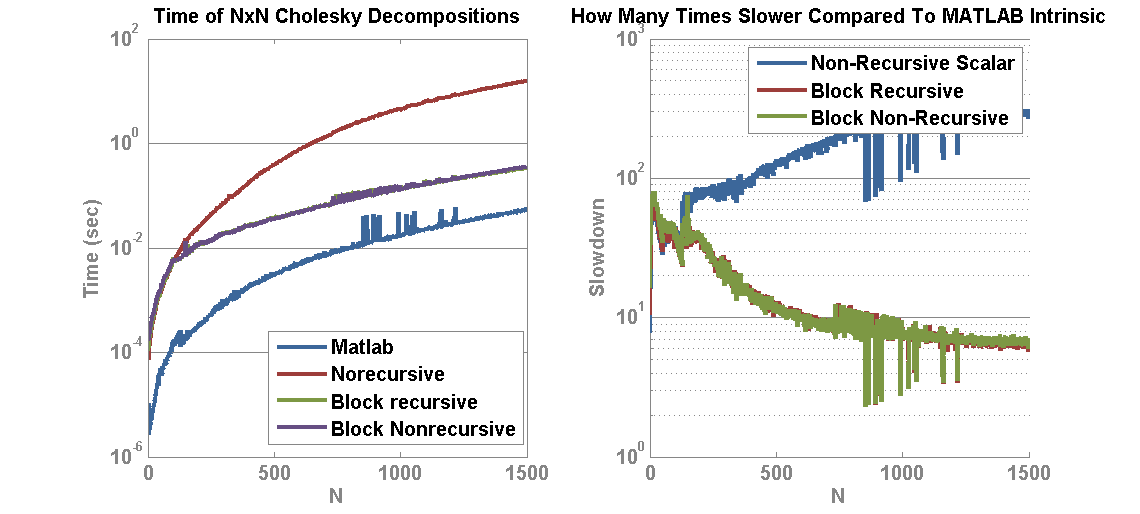
The next step is to evaluate speed of the gpuArray on a basic L1 Optimization set—l1 magic.

The code used to generate this data is as follows:


allTypes = {'Double', 'gpuArrayDouble', 'Single', 'gpuArraySingle'};
allTimes = nan(length(allTypes),1);

n = 2048;       % size of operation for Ax
num_mc = 2^10;  % number monte carlo runs to compute time average of runs

randn('seed', 1982);
Am = randn(n,n);
xm = randn(n,1);      

for ind_type = 1:length(allTypes)
   
    myType = allTypes{ind_type};
     
    switch lower(myType)
        case 'double'
            A = double(Am);
            x = double(xm);
        case 'single'
            A = single(Am);
            x = single(xm);
        case 'gpuarraydouble'
            A = gpuArray(Am);
            x = gpuArray(xm);
        case 'gpuarraysingle'
            A = gpuArray(single(Am));
            x = gpuArray(single(xm));
        otherwise
            error('Unknown type');            
    end    
    
    tic
    for ind_mc = 1:num_mc
        y = A*x;
    end
    allTimes(ind_type) =  toc/num_mc;
    
end

%% Display the results
figure(34);
clf;
bar(allTimes*1000);
set(gca, 'xticklabel', allTypes, 'color', [1 1 1]*.97);
title(['Timing of CPU and GPU in M' version('-release')]);
xlabel('Type');
ylabel('Time (ms)');
grid on

%%
figure(35);
clf;
speedupLabels = {('Double to Single') , ...
                 ('Double to gpuDouble'), ...
                 ('Single to gpuSingle'), ...
                 'Double to gpuSingle'};
bar([allTimes(1)/allTimes(3), allTimes(1)/allTimes(2),  ...
    allTimes(3)/allTimes(4), allTimes(1)/allTimes(4)]);
set(gca, 'xticklabelrotation', 15, 'xticklabel', speedupLabels, 'color', [1 1 1]*.97);
title(['Speedup of CPU and GPU in M' version('-release')]);
xlabel('Type');
ylabel('Speedup');
grid on

May 8, 2014

Z-Order Curve and Wavelets

The Z-Order (Morton) Curve describes an ordering a 2-D image in memory so that points in the image that are close in Euclidean distance are similarly close in memory. It can be compared to column-major ordering where pixels are simply lined up according to columns. This makes indexing easy but breaks all locality and can make linear transformations appear overly complex.

I wanted to visualize how this ordering changes locality be visualizing the wavelet transform that has been similarly modified to account for an image being placed in memory with the z-order curve. By placing each 2D wavelet as a row in the matrix and then displaying it as an image we get the following:

First, the Haar wavelets for an 8×8 image:

Notice how the column major ordered wavelets have large breaks that scatter the pieces of each wavelet across memory. However, the properly z-ordered image results in a stacked, block diagonal transform. Note that special care has to be taken since the wavelets are stored in levels and for the Wxx Wxy and Wyy. We stack the wavelets in an order from the largest level to smallest. Then, for each level, we group together wavelets for each pixel so that the result is the strong block diagonal patterns. For example, the row order for the matrix may be as show here:

Where we start in the top left and then for each levels quadrant we move in the z-order curve for that quadrant.

Large matrices result in more fragmented memory for column major order, while the z-ordering preserves the diagonal pattern.

For Daub8 wavelets the picture is not as clean because the nonzero terms do not fall on example powers of two, but there is still strong structure and the non-zero terms are concentrated:

The code used to create the ordering is by Ravi Lakkundi from Mathworks File Exchange (BSD License) and is:

function A = mapping(n)
% To create a Morton Scan order matrix
if n == 2
A = [1 2; 3 4];
else
B = mapping(n/2);
A = [B B+(n/2)^2; B+(n/2)^2*2 B+(n/2)^2*3];
end

February 11, 2014

Cholesky MKL Baseline

This article will attempt to establish a performance baseline for creating a custom Cholesky decomposition in MATLAB through the use of MEX and the Intel Math Kernel Library (MKL). In the past I showed a basic and block Cholesky decomposition to find the upper triangular decomposition of a Hermitian matrix A such that A = L’L. The block performed substantially better than a single term operation but still not as good as MATLAB R2013a Intrinsic Chol(…) function. The times worked out to be that the non-blocking Cholesky decomposition in MATLAB was about 200x slower than MATLAB and the Blocking was about 7x slower. Further work by Chris Turnes in porting his code to C++ showed substantial gains, and using BLAS routines rather than naive C++ improved things further. However, parity with MATLAB was still not achieved. Sources indicate that MATLAB uses the MKL internally, so I correctly expected that calling the MKL LAPACK Chol(…)-equivalent function should yield equivalent results. However, the operation is blazing fast and so care must be taken with memory management and copies in order to reach parity with MATLAB.

The Intel MKL is a fast mathematics library from Intel that includes full implementations of BLAS, LAPACK, FFT, and other operations. It widely utilizes clever optimizations and Single Instruction Multiple Data (SIMD) operations like SSE. The LAPACK routine we are interested in is

int dpotrf(char *uplo, int *n, double *a, int*lda, int *info);

where dpotrf(…) is the double precision (“d”), symmetric or Hermitian positive definitite (“po”) triangular factorization (“trf”) LAPACK routine. We wish to create an upper triangular factorization by setting uplo to “U” for upper, the dimension n and lda to the size of the matrix, and the data pointer a to a COPY of the matrix to factor because this factorization is going to happen in place.

It turns out the copy operation is best done but copying only the upper triangular part of the matrix A. A naive copy using

plhs[0] = mxDuplicateArray(A);

is a poor choice for two reasons. First, the function dpotrf(…) writes its results only in the upper triangular portion of result and leaves the rest of the matrix as is. The result is that you must zero out the lower triangular part in C++ or call triu(C) on the resulting triangular factorization in MATLAB. Doing a FULL copy and then calling triu(…) results in code that is about 15% slower than only copying the parts of A you need and then dropping triu(…). The proper code for extracting the upper part of a given matrix was written by Turnes as:

plhs[0] = mxCreateDoubleMatrix(n, n, mxREAL);
double *data = mxGetPr(plhs[0]), *prIn = mxGetPr(prhs[0]);
for (int i = 0; i < n; i++)
    memcpy(data + i*n, prIn + i*n, sizeof(double)*(i+1));

Once this is done, the LAPACK routine can be executed. As it turns out, you can run either a full copy of MKL or plug into the MATLAB version by compiling with mex and the -lmwlapack option like so:

mex cholchol.cpp -lmwlapack

Both reach parity with MATLAB for large sizes. This means that we may be able to reach parity with MATLAB using MEX code provided that we use optimized BLAS routines. For example, at size 2048 x 2048 real matrix, I obtain the following timing:

Time cholchol(…) MEX/MKL: 0.1315 s
Time MATLAB: 0.1302 s

Next, I may consider implementing the block Cholesky decomposition in C++ using basic BLAS and the rank-k updates from MKL in order to attempt to achieve parity with more custom code.

You can download the main cholchol(…) code here.

And a comparison of times for various sizes:

This code as run on Sonata:

Motherboard: Gigabyte X58U-UD3R
Processor: Intel Core i7 950 @ 3.07 Ghz (8CPU)
Memory: 8GB
OS: Windows 7
MATLAB: R2013A
Compiler: Visual Studio 2012
MKL: Intel Composer XE 2013 SP1

January 27, 2014January 27, 2014

Block Cholesky Decomposition

A substantial improvement on the prior Cholesky decomposition can be made by using blocks rather than recursing on the scalar. This allows us to work in much large chunks and even makes the recursive formulation competitive.

Here is the recursive code:


function U = chol_sec_block(A)
% Author: Stephen Conover
% Date: January 2014
% This function uses a block formulation to recursively computer the
% cholesky decomposition of a NxN hermitian matrix A.

blockSize  = min(96, length(A));

if(isempty(A))
U = [];
return;
end;

U = zeros(size(A));

% Computer the blocks:
Utl = chol_sec_nr(A(1:blockSize, 1:blockSize));
Utr = (Utl^-1)'*A(1:blockSize, blockSize+1:end);

U(1:blockSize,1:blockSize) = Utl;
U(1:blockSize,blockSize+1:end) = Utr;

% Do the recursion.
Sbr = A(blockSize+1:end, blockSize+1:end) - Utr'*Utr;
U(blockSize+1:end, blockSize+1:end) = chol_sec_block(Sbr);

end

and here is the non-recursive:

function U = chol_sec_nr_block(A)
% Author: Stephen Conover
% Date: January 2014
% This function uses a block formulation to non-recursively computer the
% cholesky decomposition of a NxN hermitian matrix A.

% check for Empty:
if(isempty(A))
U = [];
return;
end;

% Intialize output:
N = length(A);
U = zeros(size(A));

blockSize = 96;
myOffset = -blockSize;
inds = 1:blockSize;

% Loop through each chunk of blocksize:
for n = 1:N/blockSize

myOffset = (n-1)*blockSize;

Utl = chol_sec_nr(A(myOffset + inds, myOffset + inds));
Utr = (Utl^-1)'*A(myOffset + inds, (n*blockSize+1):N);

U(inds + myOffset,inds+myOffset) = Utl;
U(myOffset + inds, (n*blockSize+1):N) = Utr;

Sbr = A(myOffset+1+blockSize:N, myOffset+1+blockSize:N) - Utr'*Utr;
A(myOffset+1+blockSize:N, myOffset+1+blockSize:N)  = Sbr;

end

% finish off the rest of the computation < blockSize int he bottom right:
if(mod(N, blockSize) > 0)
U(myOffset+1+blockSize:end, myOffset+1+blockSize:end) = chol_sec_nr(A(myOffset+1+blockSize:end, myOffset+1+blockSize:end));
end

end

The following plot compares the original scalar formulation, the new block recursive/non-recursive formulation, and the MATLAB intrinsic. The MATLAB intrinsic still spanks the scripting code but I believe we may see this come close to parity when it is implemented in C++.

Example speeds at 1500 x 1500 are:

Original Custom Recursive Scalar Decomposition time: 15.79s
Custom Recursive Cholesky Block Decomposition time: 0.3571s
Custom Non-Recursive Cholesky Block Decomposition time: 0.3384s
MATLAB Intrinsic Cholesky Decomposition time: 0.0510s