Click to Download Presentation
Click to Download Presentation
L1-Magic is old interior-point library developed by Justin Romberg around 2005. It solves seven problems related to compressive sensing and the convex relaxation of L0 problems:
- Basis Pursuit ( L1 with Equality Constraints, P1):
\( \min{\lVert x \rVert_1} \text{ subject to } Ax=b \) - Decode (PA):
\( \min_{x} \lVert y-Ax\rVert _1 \) - L1 w/ Quadratic Constraints (P2):
\( \min{\lVert x \rVert_1} \text{ subject to } \lVert Ax – b \rVert \leq \epsilon \) - Dantzig Selector (D):
\( \min{\lVert x \rVert_1} \text{ subject to } \lVert A^*(Ax – b) \rVert_\infty \leq \gamma \) - Total Variation with Equality Constraints (TV1):
\( \min{TV(x)} \text{ subject to } Ax=b \) - Total Variation with Quadratic Contraints (Tv2):
\( \min{TV(x)} \text{ subject to } \lVert Ax – b \rVert \leq \epsilon \) - Dantzig TV (TVD)
In the attached presentation given to the Georgia Tech CSIP Compressed Sensing Group and the So-Called “Children of the Norm”, I show how modifications to a handful of lines of code in L1-Magic can result in
- Substantial speed improvement
- Increased Stability
- Reduced Memory Usage
To do this, I use the following limitations
- No new fundamental methods
- No MEX Allowed
- No GPU or Parallelization
The improvements are made to Basis Pursuit, L1 with Quadratic Constraints, and TV1 with various degrees of success:
- Reducing unnecessary memory allocations using sparse matrix multiplies and Hadamard products (P1)
- Exploit Low Rank Structure in matrix A using the Woodbury Identity (P2)
- Exploit Block Structure to save on processing and memory usage (Tv1)
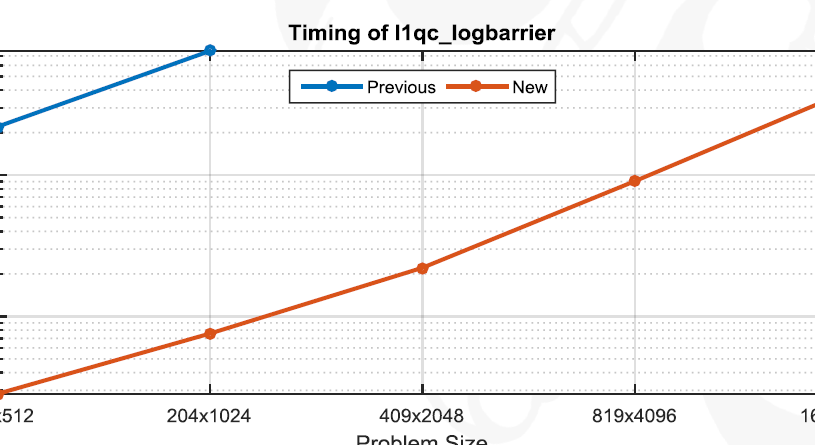
One substantial contribution is that the l1qc (P2) code displayed substantial stability issues. For low rank problems, we completely fix this issue and show ~100x speedup on certain problems. Results are dependent on the shape of A (low rank gives us better results) and incorporating these results may require switching methods between the current implementation and these proposed changes as m approaches n.